Na aula de hoje vamos a uma dúvida bem interessante. Um arquivo bitmap basicamente é uma matriz de bits que representa uma imagem – Como rotacionar uma matriz de bits em 90 e 180 graus?

Antes de qualquer coisa vamos entender que história é esta de matriz e bitmap.

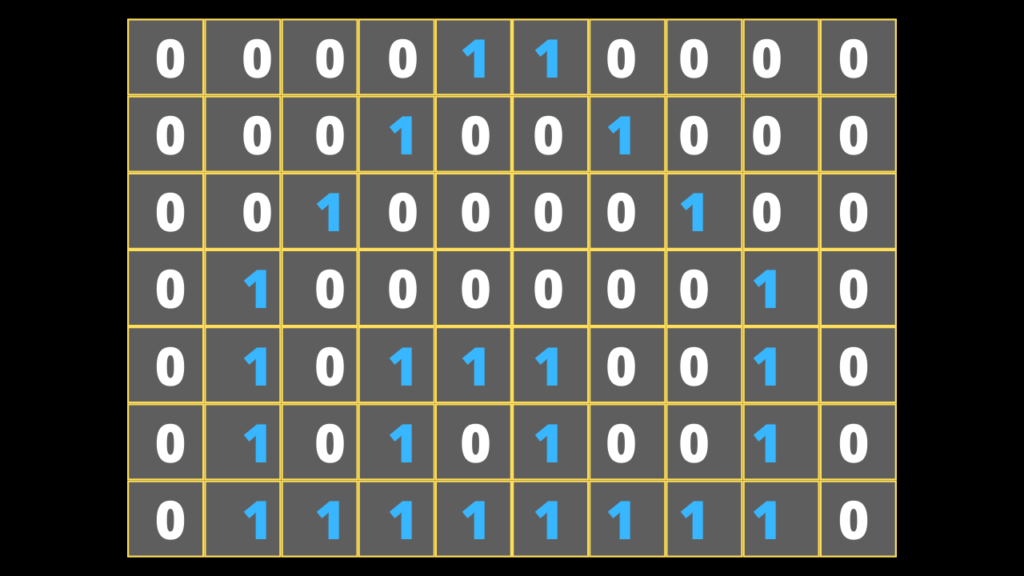
Uma imagem pode ser representada por uma matriz de bits. Como cada bit pode assumir apenas dois valores possíveis, zero ou um, estes valores são utilizados para indicar se um determinado pixel deve ou não se pintado. Observe a matriz de bits na imagem a seguir.

Para facilitar, veja a imagem a seguir, onde cada dígito 1 foi pintado de azul. Consegue perceber a formação de uma figura?

Agora, vamos fazer o que o computador faz, pintar os campos com o dígito 0 de branco e os campos com o dígito 1 de preto. O resultado é a imagem a seguir.

E a matriz fornecida para o exercício, qual imagem representa? Bem, se você imaginou isso, basta fazermos o mesmo com a matriz do exercício, branco para os campos com 0 e preto para os campos com 1 e o resultado é a imagem a seguir.

Agora precisamos rotacionar a matriz que representa esta imagem em 90 graus e 180 graus. Como fazer isso?

A primeira coisa que precisamos entender é o que significa rotacionar esta matriz. Vamos olhar para a imagem. O que significa rotacionar esta imagem em 90 graus? Basicamente é tombá-la uma vez para a direita, assim:

Como você deve ter imaginado, rotacioná-la em 180 graus é tombá-la para a direita duas vezes, assim:

Também podemos fazer rotações negativas, como por exemplo -90º. Neste caso iremos tombar a imagem para esquerda, assim:

Para entendermos como fazer isso, precisamos olhar para uma matriz. à esquerda temos a matriz original e a direita temos a matriz rotacionada em 90 graus.

Há diversas formas de fazer isso, umas mais eficientes outras nem tanto. Aqui não estou preocupado com eficiência, mas em transmitir a ideia de como fazer.

No passo a passo apresentado na imagem, perceba que cada linha da matriz original se transformou em uma coluna. A primeira linha virou a última coluna, a segunda linha virou a penúltima coluna e assim por diante.

Esse resultado pode ser obtido com duas repetições e manipulando os índices ao acessar a matriz, percorrendo a matriz original em linhas e salvando numa segunda matriz em colunas.

A seguir apresento a função que faz a rotação em 90 graus. Como a rotação é feita em uma segunda matriz, ao final a matriz rotacionada é copiada para a matriz original por meio do procedimento copiar. Observe que para rotacionar a matriz 180º basta chamar o procedimento rotacionar90 duas vezes.

	funcao rotacionar90(inteiro m[][]){
		inteiro l, c, m2[tam][tam]

		para(l = 0; l < tam; l++){
			para(c = 0; c < tam; c++){
				m2[c][tam - 1 - l] = m[l][c] // 90º
			}
		}
		copiar(m, m2)
	}

Código de exemplo completo em Portugol para rotacionar uma matriz em 90º

programa{

/*
        Código escrito por Wagner Gaspar
        Maio de 2021

*/
	const inteiro tam = 8

        // imprime uma matriz na tela
	funcao imprimir(inteiro m[][]){
		inteiro l, c
		para(l = 0; l < tam; l++){
			para(c = 0; c < tam; c++)
				escreva(m[l][c], " ")
			escreva("\n")
		}
	}

        // copia uma matriz m2 para a matriz m1
	funcao copiar(inteiro m1[][], inteiro m2[][]){
		inteiro l, c

		para(l = 0; l < tam; l++){
			para(c = 0; c < tam; c++)
				m1[l][c] = m2[l][c]
		}
	}

        // rotaciona uma matriz m para a matriz m2
	funcao rotacionar90(inteiro m[][]){
		inteiro l, c, m2[tam][tam]

		para(l = 0; l < tam; l++){
			para(c = 0; c < tam; c++){
				m2[c][tam - 1 - l] = m[l][c] // 90º
			}
		}
		copiar(m, m2)
	}
	
	funcao inicio(){
		inteiro matriz[8][8] = {
			 		{0,0,0,0,0,0,0,0},
					{0,0,1,0,0,1,0,0},
					{0,0,0,0,0,0,0,0},
					{0,0,0,0,0,0,0,0},
					{0,1,0,0,0,0,1,0},
					{0,0,1,0,0,1,0,0},
					{0,0,0,1,1,0,0,0},
					{0,0,0,0,0,0,0,0}}

		imprimir(matriz)
		rotacionar90(matriz)
		rotacionar90(matriz)
		escreva("\nMatriz rotacionada:\n")
		imprimir(matriz)
	}
}