Como comprimir dados com o Código de Huffman – Algoritmo de Huffman

Dando continuidade ao nosso Curso de Programação C, vamos aprender uma plicação prática para algumas das estruturas de dados que aprendemos aqui no curso, inclusive a árvore binaŕia.

Vamos aprender na aula de hoje como comprimir dados com Código de Huffman , também conhecido como Algoritmo de Huffman.

Cada dia produzimos mais e mais documentos digitais, sejam eles áudios, vídeos, imagens ou textos. Essa grande quantidade de documentos, e em muitas vezes grandes documentos, tornam necessário o desenvolvimento de técnicas para otimizar e/ou reduzir o uso de espaço de armazenamento não apenas em HDs e SSDs mas também, e principalmente, para o compartilhamento em rede, reduzindo a quantidade de dados trafegando em rede.

Um famoso algoritmo na literatura para compactar texto é o Algoritmo de Huffman, também conhecido como código de Huffman. É este algoritmo que iremos aprender nesta aula e desenvolveremos nas aulas seguintes.

O Algoritmo de Huffman ou codificação de Huffman foi proposto por David A. Huffman em 1952 durante seu doutorado no MIT – Instituto de Tecnologia de Massachusetts (Massachusetts Institute of Technology).

O estudo deste algoritmo neste momento é interessante por fazer uso de diversas estruturas de dados que já estudamos aqui no curso, como tabelas, listas encadeadas ou filas de prioridade e árvore binária.

Como funciona o Algoritmo de Huffman?

Basicamente o algoritmo pode ser simplificado para três passos, assim:
– Determinar a frequência de cada elemento no texto a ser comprimido;
– Montar uma árvore binária agrupando os símbolos de acordo coma frequência.
– Percorrer a árvore para codificar ou decodificar os dados.

Vamos conhecer cada uma das etapas passo a passo

Vamos tomar a seguinte frase como exemplo: “Vamos aprender a programar”

Se formos codificar esta frase usando os códigos da tabela ASCII, teremos algo assim:
V = 0101 0110
a = 0110 0001
m = 0110 1101
o = 0110 1111
s = 0111 0011
…

Perceba que com a tabela ASCII cada caracter possui um código de mesmo tamanho, 8 bits, independente de quantas vezes esse caracter ocorra no texto. Dessa forma, fazendo uma continha básica, temos:

26 * 8 = 208 bits

O total de caracteres da frase (26) vezes a quantidade de bits de cada caracter (8) nos diz que serão necessários 208 bits para armazenar nossa frase de exemplo.

Agora, vamos descobrir quanto será necessário se comprimirmos o texto com o Algoritmo de Huffman.

A primeira ação é contar a ocorrência de cada caracter e montar a tabela de frequência. Na video aula apresentada no final deste material, por engano, eu esqueci o último r da frase, então, para evitar confusão, também irei omitir o último r da nossa frase de exemplo aqui também, assim:

“Vamos aprender a programa”

Tabela de Frequência:

V = 1
a = 5
m = 2
o = 2
s = 1
‘ ‘ = 3
p = 2
r = 4
e = 2
n = 1
d = 1
g = 1

O passo seguinte é, a partir da tabela de frequência, criar uma lista encadeada ou uma fila de prioridade. A principal característica desta estrutura é que ela deve estar ordenada de forma crescente, de forma que o caracter menos frequente seja o primeiro e o mais frequente seja o último, como apresentado na figura a seguir.

fila de prioridade ordenada — Fila de prioridade ou lista encadeada ordenada de forma crescente.

Uma vez montada a estrutura de dados descrita acima, precisamos repetir algumas operações até que reste apenas um elemento na estrutura de dados. As operações são as seguintes:
– retirar os dois elementos menos frequentes (remover do início)
– Criar um novo elemento com a junção dos dois elementos removidos. A frequência deste novo elemento será a soma da frequência dos dois elementos removidos.
– Inserir este novo elemento na estrutura de dados (lista encadeada ou fila de prioridade) mantendo a ordenação correta.

A figura a seguir exemplifica a remoção dos dois elementos menos frequentes e a criação de um terceiro elemento.

código de huffman1 — Exemplo de remoção dos dois elementos menos frequentes e formação de um terceiro elemento.

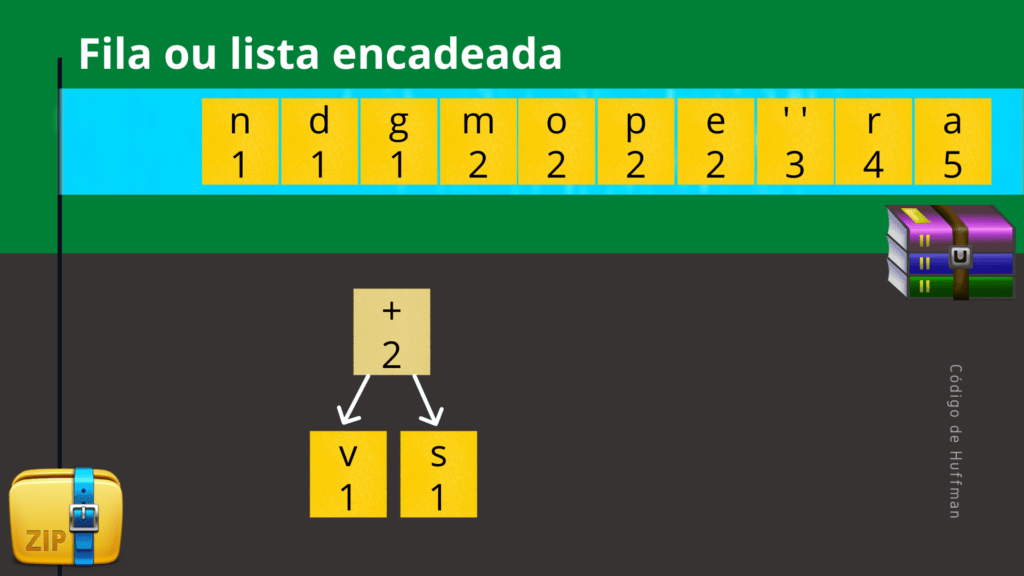
A figura a seguir apresenta o processo de inserção deste novo elemento na estrutura de dados de forma ordenada.

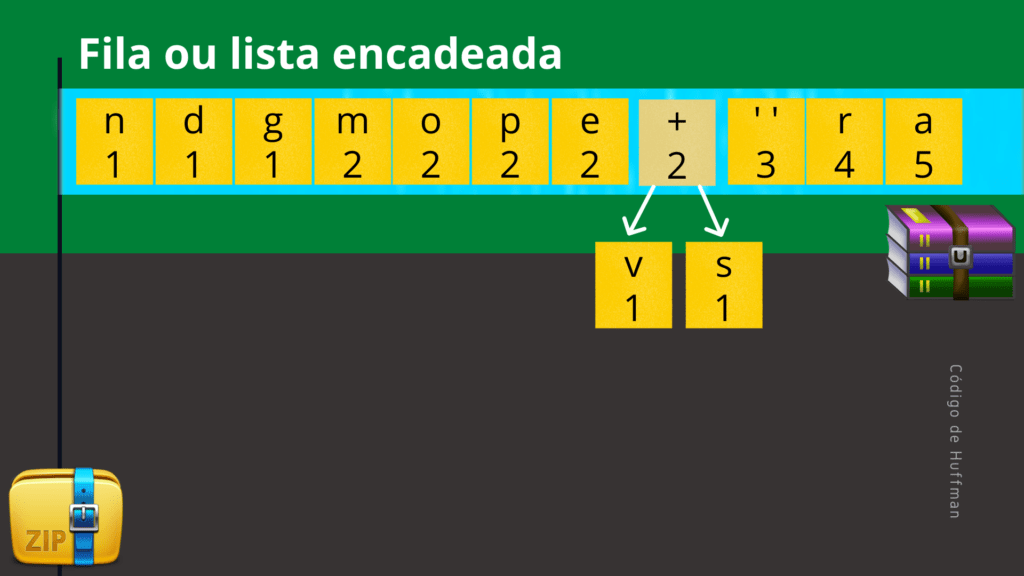
código de huffman2 — Exemplo da inserção do novo elemento mantendo a ordenação crescente.

Como dito acima, este processo deve se repetir até que reste apenas um elemento em nossa lista encadeada (fila de prioridade). Quando isso ocorrer, este único elemento será a raiz da nossa árvore de huffman. Isso fica mais evidente na figura a seguir.

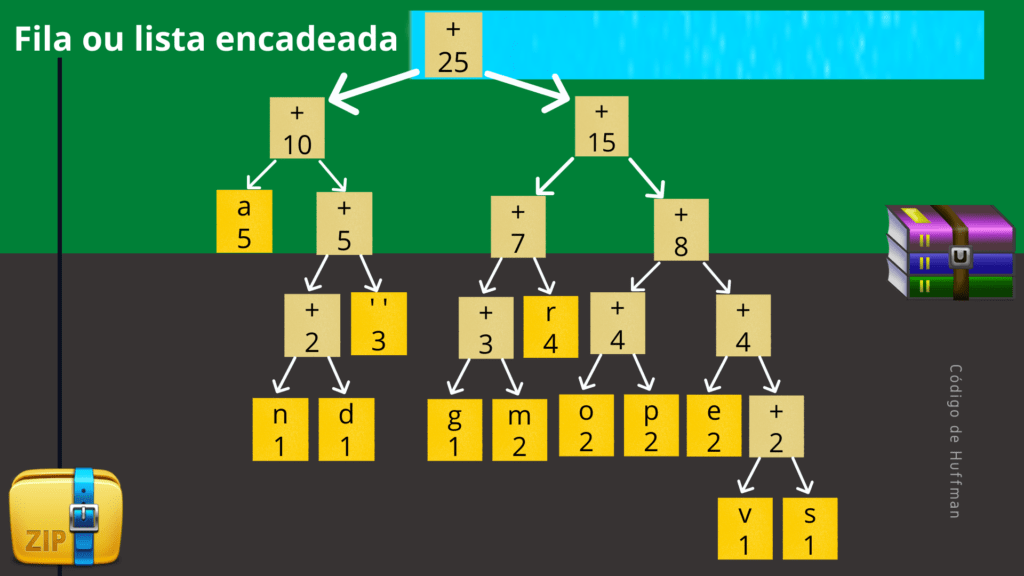
código de huffman3 — Exemplo quando resta um único elemento em nossa estrutura de dados.

Observe que os caracteres da nossa frase de exemplo ocorrem sempre em um nó folha (está lembrado do conceito de nó folha? É um nó que não possui filhos). O conteúdo dos nós intermediários é irrelevante, por isso foram representados com o sinal da soma ( + ).

Como codificar um texto com o Algoritmo de Huffman?

Agora que já temos a árvore de huffman montada, estamos prontos para codificar a nossa frase de exemplo. A ideia é não utilizar os 8 bits da tabela ASCII, mas códigos fornecidos pela árvore de huffman, que serão menores para caracteres frequentes e maiores para caracteres não frequentes.

Essa nova tabela de códigos é obtida percorrendo a árvore partindo da raiz até as folhas. Toda vez que vamos para a esquerda contamos um 0 (zero), e toda vez que vamos para a direita contamos um 1 (um). Assim, ao percorrer toda a árvore conseguimos obter novos códigos para os caracteres.

A figura a seguir mostra a tabela de códigos completa para a nossa frase de exemplo. Observe que caracteres mais frequentes possuem códigos menores enquanto caracteres menos frequentes possuem códigos maiores.

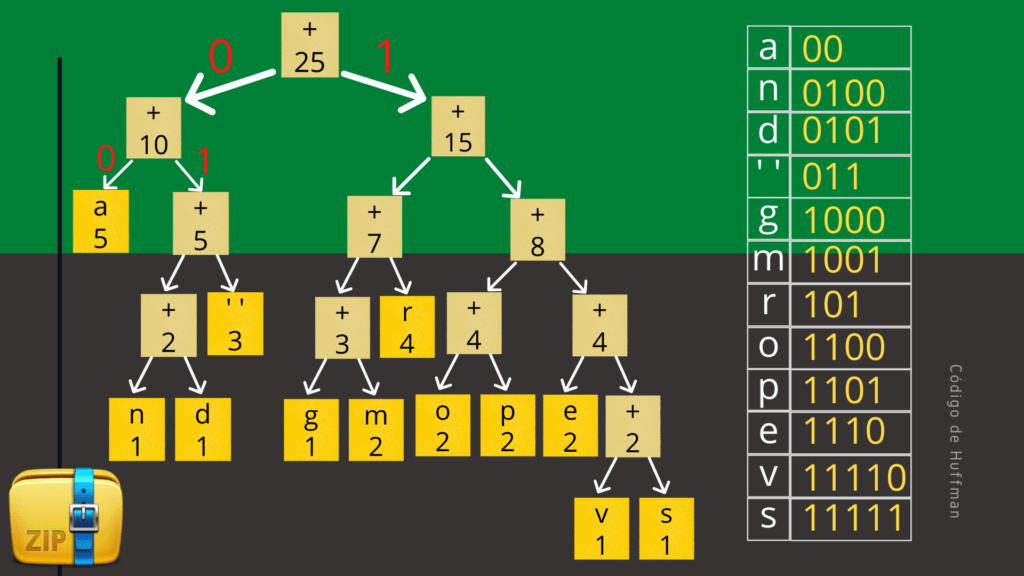
código de huffman4 — Tabela de códigos gerada com o Algoritmo de Huffman para a frase de exemplo.

Agora, para codificar o texto, basta substituir cada caracter pelo código correspondente na tabela de códigos. Contudo, qual será a melhoria? Bom, vamos calcular quantos bits serão necessários para codificar nossa frase de exemplo. Como temos a quantidade de cada um, basta multiplicar pelo tamanho do código, assim:

Tabela da quantidade de ocorrências vezes o tamanho do código

V = 1 * 5 = 5
a = 5 * 2 = 10
m = 2 * 4 = 8
o = 2 * 4 = 8
s = 1 * 5 = 5
‘ ‘ = 3 * 3 = 9
p = 2 * 4 = 8
r = 4 * 3 = 12
e = 2 * 4 = 8
n = 1 * 4 = 4
d = 1 * 4 = 4
g = 1 * 4 = 4

Total: 85 bits –> 208 – 85 = 123 bits a menos

Como decodificar um texto com o Algoritmo de Huffman?

Após o processo de codificação, nossa frase de exemplo será mais ou menos assim: 111100010011100111110110011011011110010001011110101…

Como obter o texto novamente?

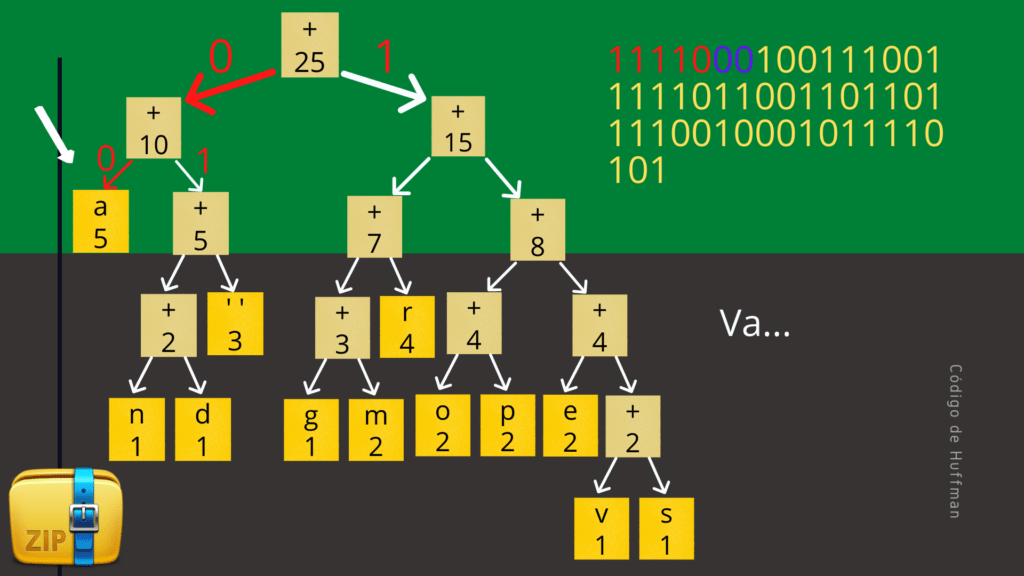
Precisamos fazer o caminho inverso. Partindo da raiz da árvore de huffman, se a sequencia possui um 0 (zero), então vamos para a esquerda, se for um 1 (um), então vamos para a direita. Precisamos ler cada bit e caminhar na árvore até encontrar um nó folha, que possui o caracter correspondente ao código que acabamos de ler. Ao encontrar um nó folha, o processo recomeça, voltando para a raiz da árvore, até terminar a sequência de bits.