Dando continuidade ao estudo da Árvore Binária de Busca Balanceada AVL, vamos aprender nesta aula como realizar a operações de rotação à direita para rebalancear nossa árvore.

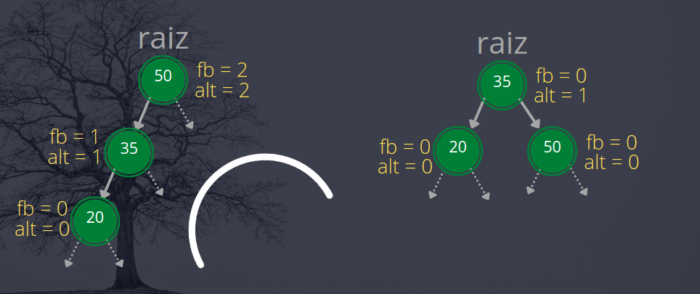
Precisamos realizar uma rotação à direita quando o fator de balanceamento for positivo. Isso indica que a nossa árvore está desbalanceada para a esquerda. Assim, a raiz da subárvore esquerda será promovida à raiz enquanto a raiz que está desbalanceada se tornará filha. Na figura a seguir temos um exemplo de uma rotação à direita. O nó 35 se torna a nova raiz da árvore enquanto o nó 50 desce e se torna filho à direita do nó 35.

Assim como a rotação que vimos na aula anterior, há uma sequência lógica a ser seguida a fim de não perder nenhum nó.

Na figura acima o nó 50 se torna filho à direita do nó 35. Contudo, quem garante que o nó 35 não possui um filho à direita? Antes de manipular os ponteiros precisamos garantir que o filho do nó 35 será salvo caso ele exista. Assim, as primeiras ações são criar um ponteiro auxiliar para o nó 35, que chamamos de y, e outro para o filho à direita do nó 35, que chamamos de f.

Agora podemos realizar a alteração dos ponteiros. O ponteiro esquerda de y aponta para r (raiz) enquanto o ponteiro esquerda de r aponta para o filho salvo na variável f.

Por fim, precisamos recalcular a altura dos nós que foram movimentados na árvore, neste caso os nós r e y, e retornar a nova raiz da árvore, o nó y.

/*
      função para a rotação à direita
*/
No* rotacaoDireita(No *r){
    No *y, *f;

    y = r->esquerdo;
    f = y->direito;

    y->direito = r;
    r->esquerdo = f;

    r->altura = maior(alturaDoNo(r->esquerdo), alturaDoNo(r->direito)) + 1;
    y->altura = maior(alturaDoNo(y->esquerdo), alturaDoNo(y->direito)) + 1;

    return y;
}

Na próxima aula veremos como implementar as rotações duplas.