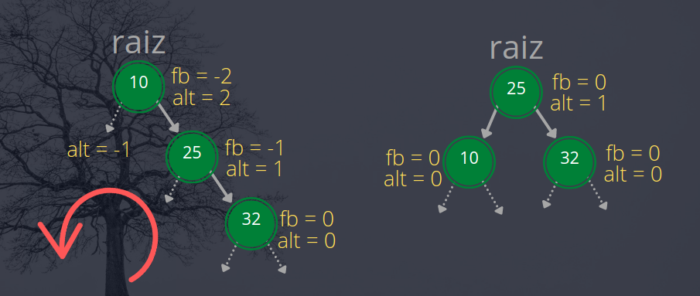
Dando continuidade ao estudo da Árvore Binária de Busca Balanceada AVL, vamos aprender nesta aula como realizar a operação de rotação à esquerda para rebalancear nossa árvore.
Desenvolver uma rotação envolve vários passos lógicos. Então, ajuda se você tiver uma figura, um desenho, que simule a rotação que você irá implementar. A figura a seguir tem exatamente este objetivo, ajudar a entender a sequência de passos a serem realizados para que a rotação ocorra sem nenhum problema.
O trecho de código a seguir apresenta a função que fará uma rotação à esquerda em nossa Árvore AVL.
Observe que há uma sequência que precisa ser seguida. Na rotação à esquerda o nó raiz deve e se tornar filho à esquerda do nó que era seu filho à direita. Contudo, quem garante que o filho à direita não possui nenhum filho? Então, a primeira ação é garantir que não iremos perder esse filho caso ele exista. A variável y aponta para o filho à direita da raiz e a variável f (de filho) aponta para o filho à esquerda de y.
Agora podemos fazer a troca. O filho à esquerda de y será o nó raiz e o filho à direita do nó raiz será o filho que salvamos na variável f.
Os nós r e y foram movidos de posição na árvore, então precisamos recalcular a altura deles. A altura de um nó na árvore é a altura de sua maior subárvore mais 1.
Por fim, observe que a raiz da árvore é alterada ao fazer uma rotação, então precisamos retornar a nova raiz, que neste caso é y.
/*
função para a rotação à esquerda
*/
No* rotacaoEsquerda(No *r){
No *y, *f;
y = r->direito; // y aponta para a subárvore direita da raiz r
f = y->esquerdo; // f aponta para o filho esquerdo de y
y->esquerdo = r; // o filho esquerdo de y passa a ser a raiz r
r->direito = f; // o filho direito de r passa a ser f
// recalcula a altura dos nós que foram movimentados
r->altura = maior(alturaDoNo(r->esquerdo), alturaDoNo(r->direito)) + 1;
y->altura = maior(alturaDoNo(y->esquerdo), alturaDoNo(y->direito)) + 1;
return y;
}
Na aula seguinte faremos a rotação à direita.