Dando continuidade ao nosso Curso de Programação C, vamos iniciar um novo módulo nesta aula. Vamos iniciar o estudo das estruturas de dados Árvores com a Árvore Binária de Busca.
A estrutura de dados do tipo Árvore forma na verdade um grande grupo de estruturas de dados. Apenas para citar algumas, temos: árvore binária de busca, árvore avl, árvore rubo negra (ou árvore vermelha e preto), árvore B.
Assim como a tabela hash, a principal utilidade das árvores é para organização e busca eficiente de dados.
Árvore Binária de Busca
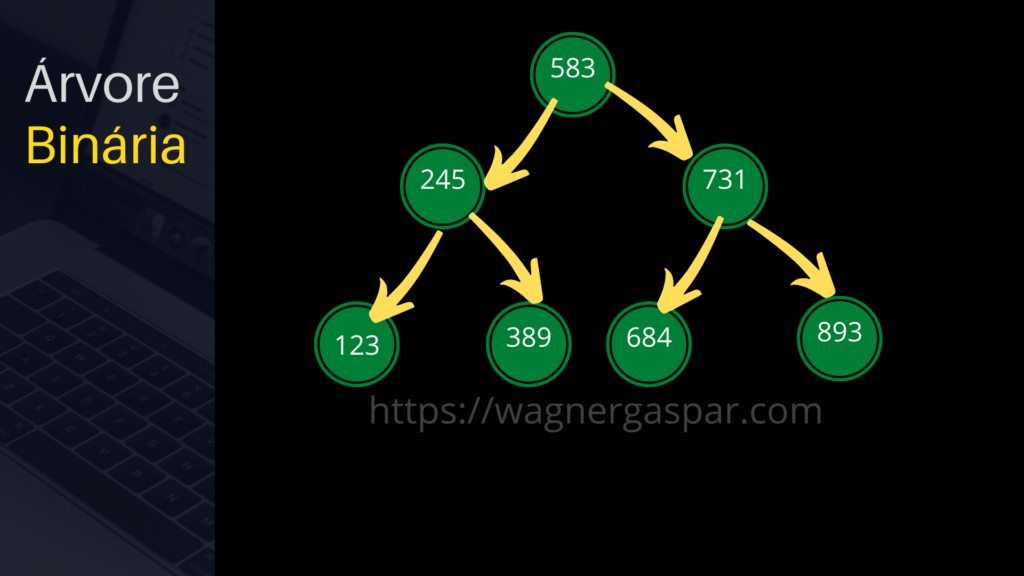
Vamos iniciar com a árvore binária de busca. A figura a seguir apresenta uma árvore binária de busca de números inteiros.
Você consegue perceber algum padrão na organização dos números?
Toda árvore possui alguns conceitos fundamentais que precisamos entender para compreender seu funcionamento. O primeiro desses conceitos é a raiz. A raiz de uma árvore (diferentemente das árvores na natureza que possuem as raízes na parte inferior, fixando-as ao solo) é o nó mais superior, ou o primeiro nó da árvore. Também existe o conceito de subárvore, neste caso quando nos referimos a uma parte da árvore e toda subárvore também possui sua raiz. Outro conceito importante é o conceito de folha. Uma folha é um nó que não possui nenhum filho.
Na árvore apresentada na figura acima, o nó com o valor 583 é a raiz da árvore. Esta árvore possui uma subárvore à esquerda com a raiz 245 e uma subárvore à direita com a raiz 731. As folhas são os nós 123, 389, 684 e 893, todos os nós que não possuem nenhum filho.
Cada nó pode ter no máximo dois filhos, um para a esquerda e outro para a direita, por isso árvore binária.
A principal característica de uma árvore binária de busca está na organização dos seus elementos. Como pode ser constatado na figura acima, em uma árvore binária os menores elementos ficam à esquerda da raiz enquanto os maiores elementos ficam à direita da raiz. É esta característica que torna o processo de busca eficiente, afinal, ao buscar um elemento, basta verificar se ele é menor ou maior que a raiz e a raiz de cada subárvore, eliminando assim a metade da árvore em cada comparação.
O processo de inserção em uma árvore binária deve obedecer este princípio a fim de manter a árvore coerente. Assim, se formos inserir o elemento 100 na ṕarvre da figura acima, ele ficará à esquerda do 123 enquanto o 700 ficará a direita do 684.
Nas próximas aulas veremos na prática como implementar uma árvore binária de busca.