Nesta aula nós ainda não iremos escrever nenhuma linha de código para implementar o Algoritmo de Huffman. Isso porque uma etapa extremamente importante e normalmente ignorada por quem está aprendendo a programar é a etapa de “pensar a solução do problema antes de codificar”.
Na aula anterior nós vimos que o Algoritmo de Huffman é composto de várias etapas ou passos lógicos e faz uso de diferentes estruturas de dados. Isso nos trás algumas perguntas:
- quantas estruturas exatamente precisamos?
- qual o tipo de cada estrutura (vetor, matriz, lista, fila, pilha, árvore, tabela hash, etc)?
- qual o tipo de dado de cada uma das estruturas?
- qual o tamanho destas estruturas?
Pensar nestas questões antes de iniciar a escrita do código pode poupar muito trabalho no futuro. É isso que faremos nesta aula.
Na aula anterior nós aprendemos que o Algoritmo de Huffman é uma sequência de passos lógicos que pode ser sintetizado mais ou menos assim:
– Criar a tabela de frequência
– Gerar uma Lista ou fila ordenada pela frequência
– Criar uma Árvore binária conhecida como árvore de huffman
– Gerar a tabela de códigos também conhecida como dicionário
– Codificar
– Decodificar
Nesta etapa é extremamente importante rabiscar, anotar ideias. Definir uma hierarquia, o que acontece primeiro? O que acontece por último? Divida o problema em partes e tente resolver cada parte por vez. O mais comum nesta etapa para quem está aprendendo é olhar para o problema de forma geral e ficar perdido, sem saber por onde começar.
Na solução que iremos desenvolver nas próximas aulas eu irei dividir o problema de compactar um texto com o algoritmo de huffman em 6 partes:
– Ler o texto a ser comprimido e gerar a tabela de frequência;
– Gerar a lista / fila (como serão os nós desta estrutura?);
– Gerar a árvore de huffman;
– Gerar a tabela de códigos (dicionário);
– Comprimir o texto;
– Descomprimir o texto.
Observe que com esta simples ação de dividir o problema em partes já conseguirmos perceber uma ordem lógica. Por exemplo, é impossível gerar a lista / fila ordenada sem antes ler o texto e gerar a tabela de frequência. Assim como não é possível gerar a tabela de códigos (dicionário) sem antes gerar a árvore de huffman.
Agora, vamos pensar na implementação de cada uma testas partes de forma individual.
1) Como gerar a tabela de frequência?
A tabela de frequência é a tabela com a quantidade de ocorrências de cada caracter no texto a ser comprimido. Como o texto pode ser grande, o ideal é que não seja necessário buscar um determinado caracter nesta tabela, mas que seja possível um acesso direto à posição que contêm a frequência do caracter. Isso é possível fazendo uso dos códigos da tabela ASCII.
Já vimos no início do curso que ao imprimirmos um caracter usando a máscara %d será impresso o código do respectivo caracter na tabela ASCII. Assim como, ao imprimir um número (no intervalo de 0 a 255) com %c, será impresso o respectivo caracter na tabela ASCII representado por aquele número.
A instrução printf(“%d”, ‘a’); irá imprimir o número 97, que é o código ASCII do caracter ‘a’, enquanto a instrução printf(“%c”, 97); irá imprimia ‘a’, que é o caracter na tabela ASCII identificado pelo código 97.
Sabendo disso, podemos criar um vetor de inteiros de tamanho 256 (índices variando de 0 a 255) para ser a tabela de frequência e inicializar esse vetor com zero. Assim, para cada caracter do texto a ser comprimido, conseguimos um acesso direto ao vetor com seu código da tabela ASCII, dispensando a necessidade de busca.
2) Gerar a lista / fila (como serão os nós desta estrutura?)
Nesta etapa precisamos gerar uma lista encadeada ou uma fila de prioridade ordenada. A estrutura em si a ser escolhida não faz muita diferença, mas o nó que irá formar esta estrutura pode fazer muita diferença e há diversas formas de fazer isso. Eu vou adotar aqui uma representação, você pode escolher uma representação diferente.
Os nós desta estrutura serão unidos de dois em dois para formar a árvore de huffman. Então, o nó desta estrutura deve possuir dois ponteiros para receber os filhos à direita e à esquerda ou, deve possuir em seu interior, um ponteiro para o nó que formará a árvore.
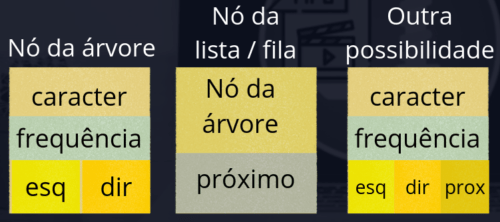
Aqui eu criarei apenas um nó com cinco campos diferentes:
– um campo para um caracter;
– um campo para a frequência do caracter;
– um ponteiro próximo a ser usado na lista / fila
– um ponteiro esquerda a ser usado na árvore;
– um ponteiro direita a ser usado na árvore.
Assim, conseguimos usar o mesmo nó na criação e manipulação das duas estruturas de dados.
3) Gerar a árvore de huffman
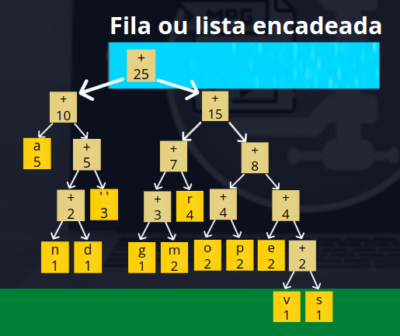
Usando a terceira representação para os nós apresentada na figura acima, fica fácil construir a árvore de huffman. Basta fazermos uma repetição para remover os dois nós de menor frequência (no início) e uni-los com um terceiro nó enquanto a quantidade de nós for maior que 1.
Quando esta repetição terminar, nossa lista / fila terá apenas um nó e este nó será a raiz da árvore de huffman, como apresentado na figura abaixo.
4) Gerar a tabela de códigos (dicionário)
Ao percorrer a árvore de huffman gerada no passo anterior conseguimos obter o novo conjunto de códigos para cada caracter. Precisamos agora de uma tabela para armazenar esses códigos. Esta tabela será o nosso novo dicionário.
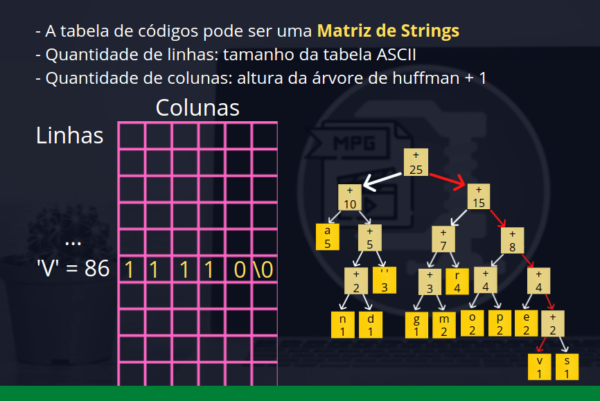
Podemos pensar esta tabela como uma matriz de strings. Como cada linha terá o código de um caracter diferente, sua quantidade de linhas será o tamanho da tabela ASCII, enquanto a quantidade de colunas será a altura da árvore de huffman + 1.
Novamente conseguimos fazer um acesso direto pelo código ASCII sem a necessidade de busca.
5) Comprimir o texto
Nesta etapa já temos o novo dicionário criado no passo anterior. Então estamos prontos para codificar o texto. Para fazer isso basta obter cada caracter do texto, buscar seu código no dicionário e ir concatenando em uma longa string. Ao final do processo, teremos uma longa string de zeros e uns que representa o texto codificado.
1111000101100010101…
Observe que gerar uma string de zeros e uns é uma possibilidade. Outra possibilidade é, para cada caracter codificado, já escrever seu código em um arquivo, assim não é necessário manter em memória uma longa string de zeros e uns.
6) Descomprimir o texto
Para decodificar precisamos da árvore de huffman montada no passo 3. O processo agora é o inverso do passo anterior. Para cada caracter codificado, verificamos se é um 0 ou um 1. Se for um zero, caminhamos para a esquerda na árvore partindo da raiz, se for um 1, caminhamos então para a direita. Quando chegarmos a um nó folha, nó sem filhos, significa que acabamos de decodificar um caracter, imprimirmos o caracter do nó folha na tela (ou concatenamos em uma longa string, ou ainda escrevemos em um arquivo) e voltamos para a raiz da árvore. Este processo será repetido até que todos os zeros e uns tenham sido lidos e decodificados.
Ao final teremos o texto original que foi codificado, sem nenhuma perda.
Nas aulas seguintes iniciaremos o processo de desenvolvimento do Algoritmo de Huffma.