Na aula anterior nós elaboramos um algoritmo recursivo para calcular o enésimo termo da sequência de fibonacci. Nesta aula irei te mostrar porque você não deve usar FIBONACCI RECURSIVO!
Recursividade é um recurso extremamente poderoso na computação. Contudo, como quase tudo na vida, nem tudo são flores. Alguns problemas são extremamente eficientes quando resolvidos com recursão, como por exemplo o fatorial. O Fibonacci é uma exceção. Neste caso, o algoritmo iterativo é muito mais superior que o algoritmo recursivo em termos de desempenho e o motivo é bem simples.
No algoritmo interativo, com repetições do tipo for ou while, o processo para calcular o enésimo termo da sequência de Fibonacci parte do início, 0 e 1, calculando o termo seguinte, até tingir o termo desejado. Perceba que cada termo é calculado uma única vez.
No algoritmo recursivo, o processo é justamente o contrário. Para calcular o enésimo termo, chamadas recursivas vão sendo feitas para calcular os termos anteriores, até atingir os termos conhecidos, 0 e 1, e então voltar desempilhando e calculando cada termo.
O problema nesse processo é que, como são necessárias duas chamadas recursivas, inúmeros termos serão calculados várias vezes, fazendo com que o computador faça o mesmo cálculo dezenas, centenas de vezes.
Imagine que o usuário deseja calcular o 10º termo da sequência de Fibonacci. Na função main será feito a primeira chamada passando o valor 10, assim:
fibonacci(10)
Aí começam os problemas. O 10º termo é a soma do 9º com o 8º. Então, são feitas essas chamadas.
10º = 9º + 8º
9º = fibonacci(8) + fibonacci(7)
8º = fibonacci(7) + fibonacci(6)
Perceba que o fibonacci(7) será calculado duas vezes, uma vez para descobrir o 9º termo e outra vez para descobrir o 8º termo. Vamos resolver mais um nível. Para descobrir o 9º termo é necessário calcular o 8º e o 7º, assim:
9º = 8º + 7º
8º = fibonacci(7) + fibonacci(6)
7º = fibonacci(6) + fibonacci(5)
Agora, ainda lá para o 10º termo, vamos calcular o 8º, assim:
8º = 7º + 6º
7º = fibonacci(6) + fibonacci(5)
6º = fibonacci(5) + fibonacci(4)
Perceba como os cálculos vão se repetindo. Antes que você pergunte se há como aproveitar estes cálculos já vai aqui a resposta. Não! Não há como aproveitar estes cálculos! Cada chamada recursiva é isolada e independente e não tem acesso à dados de outras chamadas.
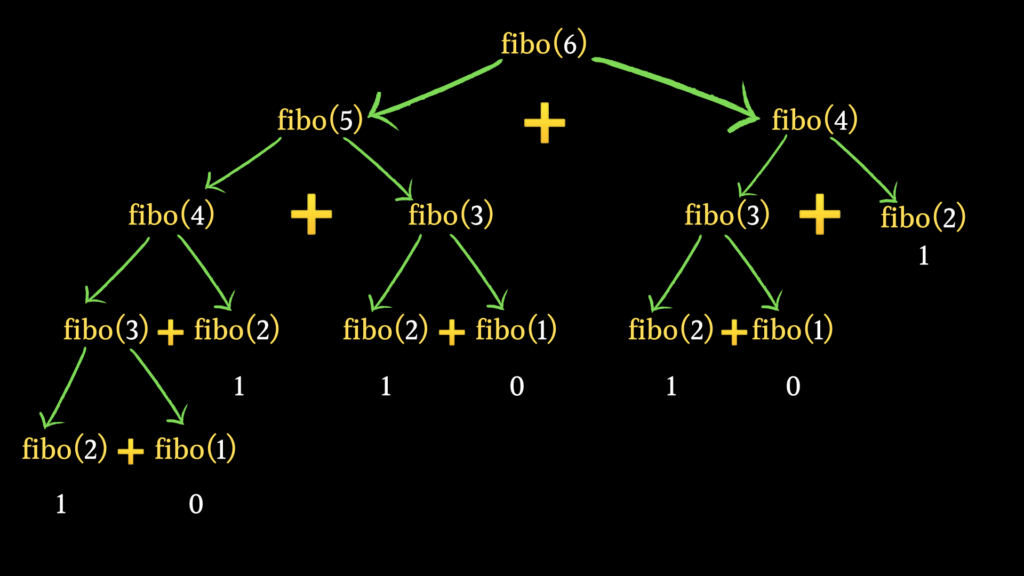
A imagem a seguir apresenta a árvore de recursão gerada para n = 6. Observe a quantidade de repetições geradas.
fibonacci(4) 2 vezes
fibonacci(3) 3 vezes
fibonacci(2) 5 vezes
fibonacci(1) 3 vezes
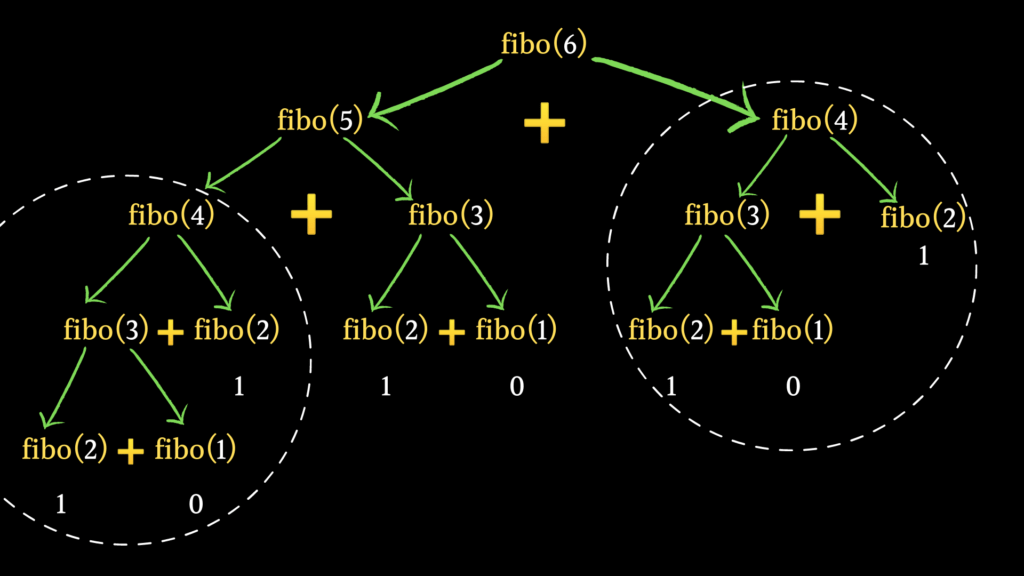
Há toda uma subárvore repetida como apresentado na figura a seguir.
Agora, imagine todo esse processo para um valor maior, 70º termo, 100º termo. Basicamente é por isso que você deve evitar utilizar o algoritmo de fibonacci recursivo.








Ótimo vídeo, explica muito bem!!!1
Que bom que ajudou 🙂
Obrigado pelo feedback.