Nas aulas anteriores nós aprendemos o conceito de recursão e vimos alguns exemplos. Contudo, será que recursão sempre será eficiente? Nesta aula nós veremos que a recursão pode ser muito custosa para o computador, realizando o mesmo cálculo inúmeras vezes. Quando isso acontece devemos procurar outra forma de resolver o problema.

Na aula anterior nós vimos como calcular um termo da sequência de fibonacci com recursão e este é um ótimo exemplo de algo que não deve ser seguido. Fibonacci recursivo é extremamente custoso para o computador resolver pois ele acaba fazendo o mesmo cálculo diversas vezes.

Lembra da pilha de recursão gerenciada pelo sistema operacional? No fibonacci recursivo nós temos duas chamadas em sequência como pode ser visto no código a seguir.

	funcao inteiro fibonacci(inteiro n){
		se(n == 1)
			retorne 0
		senao{
			se(n == 2)
				retorne 1
			senao
				retorne fibonacci(n - 1) + fibonacci(n - 2)
		}
	}

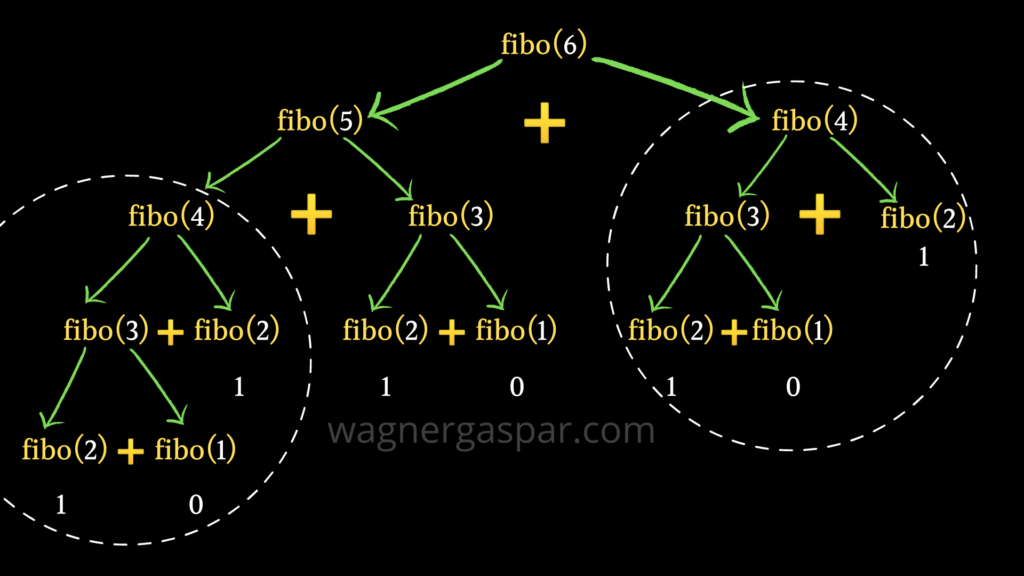
O problema é que cada chamada é independente e não tem acesso à cálculos feitos por outras chamadas separadas, apenas ao valor que é retornado pela chamada imediatamente seguinte. Assim, ao montarmos uma árvore de recursão para este problema, fica evidente a repetição de cálculos, como pode ser visto na fira a seguir.