Bora continuar nosso jogo da velha?

Se você chegou até aqui por acaso e perdeu o início não se preocupe, você pode acessar a parte I aqui e a parte II aqui.

Hoje construiremos quatro funções para identificar a vitória de um dos jogadores. Mas, porque quatro funções?

Bom, como mencionei nas partes anteriores, quanto menor for o problema mais fácil para resolvê-lo. Assim, dividiremos a verificação da vitória em quatro partes, as quatro possibilidades de vitória existentes, como apresentado na figura abaixo:

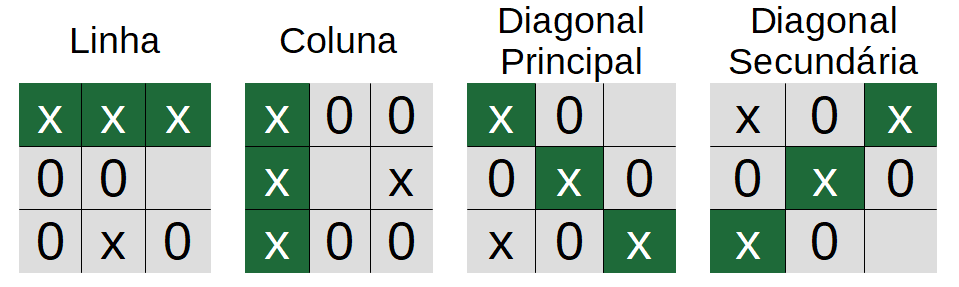
1) Vitória em uma das linhas;

Esta verificação é bem simples se você já entendeu como percorrer uma estrutura de dados do tipo matriz. Basicamente o que fazemos aqui é percorrer cada uma das três linhas da matriz, comparando o caractere de cada posição com o caractere seguinte. Um jogador vence quando qualquer uma das linhas possuir três x ou três 0.

Abaixo apresentamos a função que faz esta verificação. Seu retorno será 1 caso encontre uma linha com três caracteres iguais ou 0 caso verifique as três linhas da matriz e nenhuma possua três caracteres iguais.

int ganhouLinhas() {
    int i, j, igual = 1;
    for(i = 0; i < 3; i++) {
        for(j = 0; j < 2; j++) {
            if(eValido(jogo[i][j]) && jogo[i][j] == jogo[i][j+1])
                igual++;
        }
        if(igual == 3)
            return 1;
        igual = 1;
    }
    return 0;
}

2) Vitória em uma das colunas;

Esta verificação é muito semelhante à anterior, com a diferença que agora verificaremos as colunas. Basicamente o que fazemos aqui é percorrer cada uma das três colunas da matriz, comparando o caractere de cada posição com o caractere seguinte. Um jogador vence quando qualquer uma das colunas possuir três x ou três 0.

Abaixo apresentamos a função que faz esta verificação. Seu retorno será 1 caso encontre uma coluna com três caracteres iguais ou 0 caso verifique as três colunas da matriz e nenhuma possua três caracteres iguais.

int ganhouColunas() {
    int i, j, igual = 1;
    for(i = 0; i < 3; i++) {
        for(j = 0; j < 2; j++) {
            if(eValido(jogo[j][i]) && jogo[j][i] == jogo[j+1][i])
                igual++;
        }
        if(igual == 3)
            return 1;
        igual = 1;
    }
    return 0;
}

3) Vitória na diagonal principal;

Agora, diferentemente das duas funções anteriores, precisamos percorrer a matriz na diagonal principal, comparando cada elemento da diagonal principal com o elemento seguinte. Como os índices para acessar a diagonal principal pode ser obtida com uma única variável, fazemos uso de apenas um comando “para”.

Abaixo apresentamos a função para esta verificação, retornando 1 caso os três caracteres sejam iguais ou 0 caso contrário.

int ganhouDiagonalPrincipal() {
    int i, igual = 1;
    for(i = 0; i < 2; i++) {
        if(eValido(jogo[i][i]) && jogo[i][i] == jogo[i+1][i+1])
            igual++;
    }
    if(igual == 3)
        return 1;
    else
        return 0;
}

4) Vitória na diagonal secundária.

Por fim, precisamos também verificar a diagonal secundária. Esta é a mais trabalhosa, exigindo uma certa “brincadeira” com os índices de acesso à matriz. Caso tenha dificuldade em entender como chegamos à conta feita dentro dos pares de colchetes, assista ao vídeo no final do post ou tente desenhar no papel uma matriz com três linhas e três colunas, identificando os índices de cada posição. Você deverá chegar a algo parecido com:

00  01  02
10  11  12
20  21  22

Perceba que a diagonal secundária possui os índices 0 2, 1 1 e 2 0. São este índices que precisamos gerar. Abaixo apresentamos esta função, retornando 1 caso haja um vencedor e 0 caso contrário.

int ganhouDiagonalSecundaria() {
    int i, igual = 1;
    for(i = 0; i < 2; i++) {
        if(eValido(jogo[i][3-i-1]) && jogo[i][3-i-1] == jogo[i+1][3-i-2])
            igual++;
    }
    if(igual == 3)
        return 1;
    else
        return 0;
}

Se ficou alguma dúvida, compartilhe nos comentários que faremos o possível para esclarecer. Um grande abraço, bons estudos e até o próximo.