Dando continuidade à nosso Curso de Programação C, vamos ver nesta aula uma introdução às Árvores Balanceadas. Nas aulas seguintes veremos como implementar uma Árvore Binária de Busca Balanceada popularmente conhecida como Árvore AVL.
Para compreender uma Árvore AVL e mesmo para entender porque precisamos de árvores balanceadas é fundamental que você tenha entendido as Árvores Binárias de Busca. Então, caso tenha ficado alguma dúvida sobre Árvores Binárias, revise as aulas anteriores. Se necessário, poste suas dúvidas nos comentários ao final de cada aula.
Playlist Árvore Binária de Busca no Youtube e aqui no blog.
Playlist Curso Completo de Programação C no YouTube e aqui no blog.
Antes de iniciar a teoria sobre Árvore Balanceada, talvez você esteja se perguntando: qual o problema com as Árvores Binárias?
E esta resposta é bem simples. Uma Árvore Binária pode estar desbalanceada ou, como normalmente é chamada uma árvore binária desbalanceada, pode estar degenerada.
Mas o que é uma Árvore Binária Degenerada?
Vamos a um exemplo e logo você entenderá.
Imagine que, em uma árvore binária vazia, inserimos o valor 10, que será a raiz da árvore. Depois o valor 20, depois o valor 30, e continuamos a inserir novos elementos sempre maiores que os anteriores. Observe que os valores inseridos estão ordenados de forma crescente. Você consegue imaginar, desenhar, a árvore resultante?
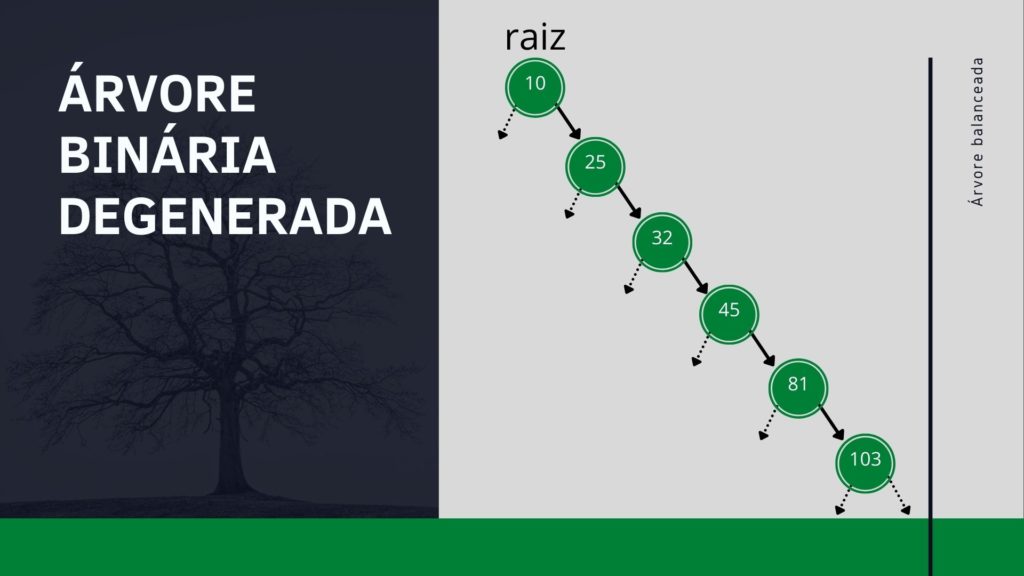
Este é o pior cenário possível para uma árvore binária. O resultado final após todas as inserções será uma árvore semelhante à apresentada na figura a seguir.
Observe que, como cada novo elemento inserido era maior que os anteriores, a árvore binária fica semelhante a um vetor, ou a uma lista encadeada e assim perdemos os benefícios proporcionados por uma árvore binária. Perceba que agora, para saber se o 500 está ou não na nossa árvore, precisamos percorrer todos os elementos, igual a uma busca sequencial em vetor ou lista encadeada.
Nos referimos a uma árvore como a apresentada na figura acima como uma Árvore Desbalanceada ou Degenerada, pois não há equilíbrio entre suas subárvores, fazendo com que uma das subárvores fique desproporcional em relação à outra. Se o objetivo de uma Árvore Binária de Busca é tornar o processo de busca mais eficiente que em vetor e listas encadeadas, uma árvore degenerado pode prejudicar todo o trabalho. Por isso precisamos de Árvores Balanceadas.
O que é uma Árvore balanceada?
Uma árvore balanceada nada mais é que uma árvore que se mantêm balanceada, ou seja, mantêm o equilíbrio entre suas subárvores, evitando assim que a árvore se assemelhe a um vetor ou a uma lista encadeada.
Toda inserção e remoção pode desbalancear a árvore uma vez que altera a quantidade de nós. Assim, para manter a árvore balanceada é necessário realizar alguns passos chamados de rotações.
Existem diversos tipos de Árvores Balanceadas: Árvore AVL, Árvore vermelho e preto (rubro negra); Árvore 2-3-4; Árvore AA; Árvore scapegoat; Árvore splay são alguns exemplos.
Nós vamos estudar a Árvore AVL proposta em 1962 por Adelson-Velskii e Landis que possui um custo de O(log(N)), melhor que uma árvore não balanceada que tem um custo de O(N).
Árvore Binária de Busca Balanceada AVL
O termo balanceada pode ser entendido como sinônimo de equilibrada. O objetivo é manter as subárvores com a menor diferença possível e esta menor diferença possível é 1 na altura das subárvores.
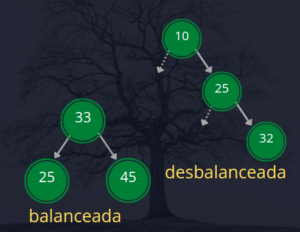
A figura a seguir apresenta duas árvores binárias, uma balanceada e outra desbalanceada.
Para descobrir se uma determinada árvore binária está ou não balanceada precisamos calcular o fator de balanceamento para cada nó da árvore.
O que é o Fator de Balanceamento de um nó?
O fator de balanceamento de um nó da árvore binária é um valor inteiro que dirá se a árvore está ou não balanceada. Seu cálculo é bastante simples sendo o resultado da subtração da altura das subárvores esquerda e direita, assim: fb = altEsq – altDir.
O fator de balanceamento aceitável para qualquer nó da árvore é 1 ou -1. Acima de 1 ou abaixo de -1 significa que a árvore está desbalanceada a partir daquele nó e é necessário realizar uma ou mais rotações para rebalancear a árvore.
Rotação simples a Esquerda
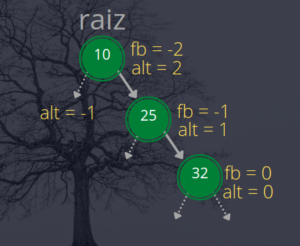
Observe a árvore apresentada na figura a seguir.
Aplicando a fórmula fb = altEsq – altDir para o fator de balanceamento (fb) de cada nó temos que o nó 32 possui o fb igual a 0. O nó 25 possui um fb igual a -1 e, por fim, o nó 10 possui um fb igual a -2, que excede o limite aceitável de 1 ou -1. Assim, a árvore está desbalanceada a partir do nó 10.
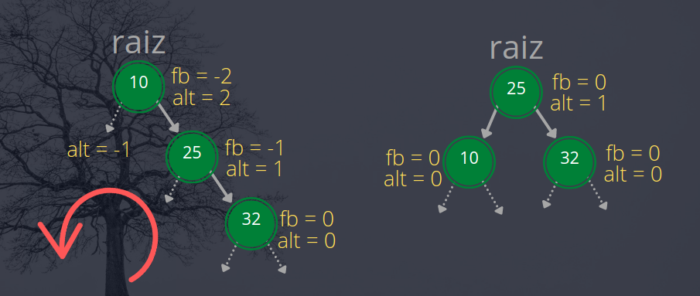
Como o fb é negativo, significa que a árvore está desbalanceada à direita, ou seja, ela pende para a direita, por isso precisamos fazer uma rotação para a esquerda. O nó 25 será promovido à raiz da árvore e o nó 10 será filho à esquerda do nó 25, como apresentado na figura a seguir.
Rotação simples a Direita
Esta rotação é análoga à anterior. É necessário uma rotação simples à direita quando temos um fb igual a 2. Neste caso a árvore pende para a esquerda, como apresenta a figura a seguir.
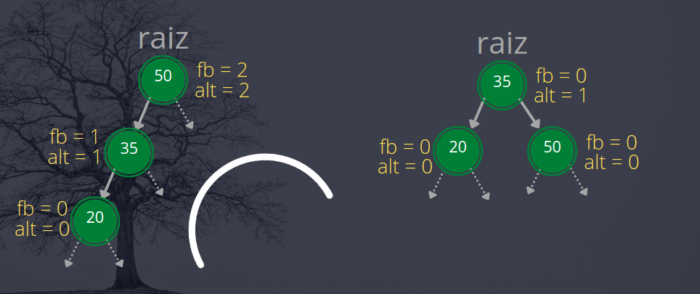
Assim como ocorreu na rotação anterior, o nó 35 será promovido à raiz da árvore enquanto o nó 50 se tornará filho à direita do nó 35.
Contudo, as rotações simples não resolvem todas as situações. Em algumas situações serão necessário rotações duplas.
Rotação Dupla Direita Esquerda
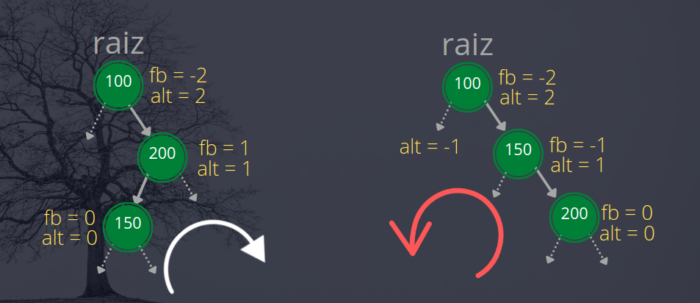
As rotações simples são utilizadas quando a árvore pende completamente para a direita ou para a esquerda. Contudo, há situações em que isso não ocorre, como na árvore apresentada na figura a seguir no lado esquerdo.
O fator de balanceamento da arvore apresentada na figura a esquerda é -2, isso indica que ela pende para a direita. Contudo, perceba que ela não pende completamente para a direita. O nó 200 pende para a direita mas o nó 150 pende para a esquerda. Quando ocorre esta situação, o nó desbalanceado será negativo (-2) e seu filho à direita terá um fb positivo (1), o que indica a inversão do sentido do desbalanceamento.
Neste caso precisamos realizar duas rotações:
1ª – Rotação à direita no filho à direita (nó 200)
2ª – Rotação à esquerda no nó desbalanceado (nó 100)
Observe que quando rotacionamos o filho à direita para a direita, invertemos a posição dos nós 200 e 150. Dessa forma, fazemos com que a árvore penda completamente para direita e então podemos aplicar uma rotação à esquerda, promovendo o 150 a raiz e rebaixando o 100 a filho à esquerda do 150.
Rotação Dupla Esquerda Direita
Esta rotação é análoga à anterior invertendo apenas o sentido do desbalanceamento. Conforme podemos observar na figura a seguir, precisamos de uma rotação à esquerda e outra a direita quando o desbalanceamento é no sentido da esquerda (2) e depois direita (-1).
Observe que o nó raiz 200 possui um fb igual a 2 enquanto seu filho à esquerda, o nó 100, possui um fb igual a -1.
Neste caso, faremos uma rotação à esquerda no filho à esquerda, trocando os nós 100 e 150. Assim, obtemos uma árvore pendendo completamente à esquerda, bastando uma rotação à direita na raiz 200 para balancear a árvore.
É muito importante que você tenha entendido o que é e como funciona uma Árvore AVL, pois na próxima aula vamos iniciar a implementação desta árvore. Se ficou alguma dúvida registre no espaço para comentários abaixo.